Zweierkomplementdarstellung

Die Zweierkomplementdarstellung ist eine Möglichkeit negative Zahlen im Binärsystem darzustellen ohne diese mit + oder - zu kennzeichnen.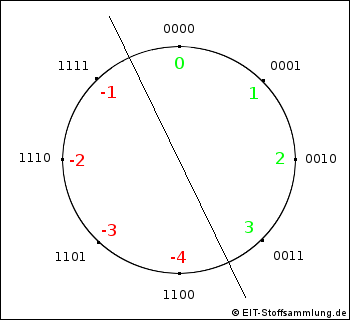



Das Zweierkomplement ist das Ergebnis aus der Bildung des Einerkomplements mit anschließender Addition von 1

• alle Zahlen haben eine konstante Stellenzahl und werden wenn nötig mit  0 aufgefüllt
• das Erste Bit kennzeichnet das Vorzeichen
• benötigt keine Fallunterscheidung bei negativen oder positiven Zahlenoperationen
• keine Unterscheidung von Vorzeichenbit und Bits bei der Zweierkomplementdarstellung
• die Zahl 0 kommt nur einmal vor
• werden auch signed binary numbers oder signed integers genannt
• alle heute üblichen Rechner arbeiten im Zweierkomplement

• Summanden sind positiv
  • die Vorzeichen beider Zahlen sind 0
  • Vorzeichen des Ergebnis muss 0 sein, ansonsten wurde der Zahlenbereich (wird von der Anzahl der Bit bestimmt) überschritten

• Summanden sind negativ
  • die Vorzeichen beider Zahlen sind 1
    
  • Vorzeichen des Ergebnis muss 1 sein, ansonsten wurde der Zahlenbereich überschritten

• Summanden mit unterschiedlichen Vorzeichen
  
  • Vorzeichen wird von betragsmäßiger größe bestimmt
    
  • Übertrag an erster Stelle wird nicht beachtet

1. Zweierkomplementdarstellung von -6 erzeugen, indem das Einerkomplement gebildet wird (Umkehrung der Stellen) und dann eine 1 addiert wird  >>>  1010
2. Jetzt addieren wir 3 + (-6)  (binär)  >>> 1101
3. Das erste Bit zeigt dass es sich bei dem Ergebnis um eine negative Zahl handelt.
4. Jetzt berechnen wir den Betrag indem wir das Zweierkomplement von 1101 bilden >>> 0011 = 3 
5. Das Ergebnis ist negativ und hat den Betrag von 3 >>> Das Ergebnis der Berechnung ist -3